4283. Stepan and pairs
Stepan is interested in the greatest common
divisor of a pair of numbers, specifically GCD(x, y). Given an integer n, Stepan wants
to know how many pairs of integers (i, j) exist such that 1 ≤ i, j ≤ n and the equation i = GCD(i, j) is satisfied.
Input. One integer n (1 ≤ n ≤ 106).
Output. Print the number of required pairs.
|
Sample
input |
Sample
output |
|
4 |
8 |
SOLUTION
number theory
Algorithm analysis
Let’s fix j (for example j = 12) and find the number of i
such that i = GCD(i, 12).
The values of i that satisfy this equation are i = 1, 2, 3, 4,
6, 12. So, any i that is a divisor of 12 satisfies the
equation i = GCD(i, 12).
The number of
such i for which i = GCD(i, j) is equal to the number of divisors
d(j) of j. Since 1 ≤ j
≤ n, we need to find the count of all divisors
of numbers from 1 to n. In other words, we need to find the sum
d(1) + d(2) +… + d(n). However, calculating d(n) requires factoring the number n, so direct computation of this sum takes O(n
) time.
Let’s look at the sum of divisors in a different way. Among the
divisors of numbers from 1 to n, one
appears 
times, two appears 
times, and so on (the
divisor i appears 
times). The number of required pairs
of integers is
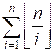
This sum can be computed
in O(n) time.
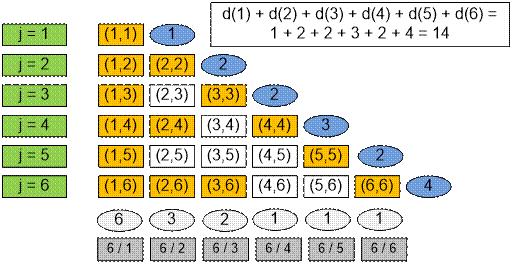
Example
For n = 6 we have the next pairs:
The number of pairs is 6 / 1 + 6 / 2 + 6
/ 3 + 6 / 4 + 6 / 5 + 6 / 6 =
= 6 + 3 + 2 + 1
+ 1 + 1 = 14
Algorithm realization
Read the value of n.
scanf("%d",&n);
Compute the answer using
the formula and print it.
s = 0;
for(i = 1; i <= n; i++)
s += n / i;
printf("%d\n",s);
Java realization
import java.util.*;
class Main
{
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
int n = con.nextInt();
int s = 0;
for(int i = 1; i <= n; i++)
s += n / i;
System.out.println(s);
con.close();
}
}
Python realization
Read the value of n.
n = int(input())
Compute the answer using
the formula and print it.
s = 0
for i in range(1,n+1):
s += n // i
print(s)